小話Vol.4：「コホモロジー」の意味を考える①

こんにちは！ルシアンです。

今日は、Twitterにて宣言していた「コホモロジー」の記事を書きたいと思います^ ^

みなさんは「コホモロジー」という言葉を聞いたことがあるでしょうか？

「コホモロジー」はトポロジーの研究から誕生した概念で、今では多くの数学の中に見いだされ、分野を問わず大事な存在となっています。

しかし、双対をなす「ホモロジー」に比べると、「コホモロジー」はイメージするのが難しく、なかなか親しみがもてないという人も多いかもしれません>_<

そこで本日は、

「昨日よりコホモロジーと仲良くなる」

を目標に、コホモロジーの幾何的な意味について考えてみたいと思います！

※この記事は「単体複体のホモロジー」を勉強したことがあると、大分読みやすくなると思います。

「勉強したことない」という方は、先に佐野岳人さんの記事

taketo1024.hateblo.jp

を読むことをオススメします^ ^♪

曲面上で、‘‘エネルギー”を観測する

今日は簡単のため、三角形で分割された曲面のみを扱っていきます。

具体例としては、「正方形から正方形を切り取った」ような次の図形を考えてみましょう。

f:id:Lucien0308:20180428183419g:plain

この図形は、

頂点(vertex)： $v_1, v_2, \ldots$
辺(edge)： $e_1, e_2, \ldots$
面(face)： $f_1, f_2, \ldots$

で構成されているとみることができます。

これから、この曲面を舞台にして、

「様々な‘‘エネルギー”を観測する」

ということを考えてみましょう。

観測方法は３種類

そもそも「いきなり‘‘エネルギー”ってなに??」と思ったかもしれませんが、具体例としては色んなものが当てはまります。

この具体例は、「３つの異なる観測方法」を説明する中で紹介しましょう^ ^

（今回は、３つの観測方法のうちの２つを紹介します！）

観測①：‘‘各地点におけるエネルギー”を観測する

まず、もっとも素朴な観測方法として、

「‘‘各地点におけるエネルギー”を観測する」

ということを考えましょう。

この具体例としては、「高さ」を考えるのが最も分かりやすいかもしれません。

そして、実際に‘‘エネルギーを観測する地点”として、全ての頂点を観測地とすることにします。

例えば、具体的な観測結果として次の図を考えてみましょう。

f:id:Lucien0308:20180428222901g:plain

このような観測結果が得られたとすると、例えば

「右下が海で、上側が高台なのかな」

「右下から左上までの最も緩やかな経路はどれだろう？」

などと想像を膨らませる事もできますね。

このような観測方法で得られた結果から、「頂点全体の集合」上の関数

$\varphi :\{v_1, v_2, \ldots \} \to \Bbb{R}$

が得られます。この $\varphi$ を０次コチェインと呼びます。*1

観測②：２地点間の‘‘向きのあるエネルギー”を観測する

次は、

「２地点間の‘‘向きのあるエネルギー”を観測する」

という方法を考えましょう。

これは、上の例の「高さ」に合わせるなら「標高の変位」や「勾配」と見なすのがふさわしいでしょう。

他にも、「風力」や「磁力」などでもよいです。

そして、この‘‘向きのあるエネルギー”の観測地点として、全ての辺を観測地とすることにします。

例えば、具体的な観測結果を図に描くと次のようになります。

（このとき、各辺には向きが指定されていることに注意してください。）

f:id:Lucien0308:20180429002451g:plain

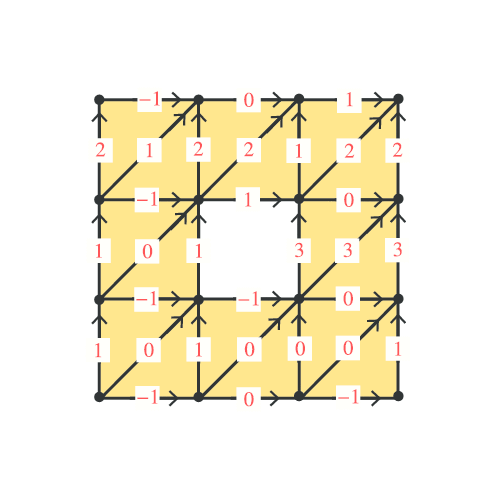
そしてこの観測方法からは、「辺全体の集合」上の関数

$\psi :\{e_1, e_2, \ldots \} \to \Bbb{R}$

が得られます。この $\psi$ を１次コチェインと呼びます。

「０次コチェイン」から「１次コチェイン」を得る

ここまで２種類の‘‘エネルギーの観測方法”と、その観測結果として得られる写像

０次コチェイン $\varphi :\{v_1, v_2, \ldots \} \to \Bbb{R}$

１次コチェイン $\psi :\{e_1, e_2, \ldots \} \to \Bbb{R}$

を見てきましたが、これらには次の関係があります。

事実：０次コチェイン $\varphi$ ごとに、１次コチェイン $\delta \varphi$ を構成できる。

この構成を実際に見ていきましょう。

いま、一つ $e_i$ という辺を選んだとします。

さらに、この $e_i$ に向きを指定して、頂点 $v_{i_1}$ から頂点 $v_{i_2}$ に向かっていると見なします。

f:id:Lucien0308:20180429011532g:plain

このとき、「 $v_{i_1}$ から $v_{i_2}$ への $\varphi$ の変化量」を $\delta \varphi$ と定義します。特に、数式にすると

$\delta \varphi (e_i) := \varphi(v_{i_2}) -\varphi(v_{i_2})$

となります。

これを全ての辺に実行すれば、１次コチェイン $\delta \varphi$ が得られるわけです。

実際、上に示した1次コチェインの具体例は、実は先に示した０次コチェインから構成したものになっていました。

今一度見比べてみて下さい＾＾

このように、０次コチェイン $\varphi$ から得られる１次コチェイン $\delta \varphi$ を１次コバウンダリと言います。

コサイクル条件＝「局所的な‘‘エネルギー保存則”」

ここで、次のような問題を考えてみましょう。

問題： $\delta \varphi=0$ （全てを０に写す関数）となるような $\varphi$ はどんな０次コチェインか？

この問題を解こうとして０次コチェインを全部調べようとすると埒が明かないので、

「 $\delta \varphi=0$ 」

という条件を少しじっくり考えてみましょう。

「 $\delta \varphi=0$ 」が成り立つということは、

全ての辺 $e_i$ について

$\varphi(v_{i_2}) - \varphi(v_{i_1}) = \delta \varphi(e_i)=0$

つまり

$\varphi(v_{i_1}) = \varphi(v_{i_2})$

が成り立つことを意味しています。

これを言葉で表すと、

「辺で結ばれた頂点の間では、 $\varphi$ の値は変化しない」

ということになります。また、別の言い方をすると、

「辺で結ばれた頂点の間では、 $\varphi$ の保存則が成り立つ」

とも捉えられますね。

この考察を私たちの具体例に当てはめてみましょう。

この具体例には頂点が１６個ありますが、全ての頂点はいくつかの辺をつないでいくことで結ぶことが出来ます。したがって、結果的に

$\varphi(v_1)= \varphi(v_2)= \cdots = \varphi(v_{16})$

が成り立つことが分かります。

この結論をまとめると、この具体例の場合は

「 $\delta \varphi=0$ $\Rightarrow$ $\varphi$ は定数関数」

という結論が得られます。

f:id:Lucien0308:20180429023522g:plain

一般に、条件「 $\delta \varphi=0$ 」をコサイクル条件といい、コサイクル条件を満たす０次コチェインのことを０次コサイクルといいます。

そして０次の場合は、この０次コサイクルの集合がそのまま０次コホモロジー群 $H^0$ となります。

例えば、この具体例の $H^0$ は

$H^0 = \{$ 実数値の定数関数全体 $\} \cong \Bbb{R}$

を満たしています。*2

「大域的に保存則が破綻する」 $\Rightarrow$ 「世界に‘‘隔たり”がある」

では、

「 $\delta \varphi=0$ $\Rightarrow$ $\varphi$ は定数関数」

という結論は、これまで考えてきた具体例以外でも通用するのでしょうか？

実は、そう単純にはいきません。そして、ここに

コホモロジーが世界の形を測る力

の一端を見ることが出来ます。

例えば、今まで考えてきた例について、中央の４つの三角形を取り除いてみましょう。

そして、

頂点 $v$ が左側の島に属するなら、 $\varphi(v)=0$
頂点 $v$ が右側の島に属するなら、 $\varphi(v)=1$

というルールで $\varphi$ を定めます。

f:id:Lucien0308:20180429033016g:plain

すると、この $\varphi$ は定数関数ではないですが、 $\delta \varphi = 0$ を満たすのです。

これは、

「左の島と右の島を結ぶ辺が存在しない」＝「世界が連結していない」

という事実をコホモロジーが捉えていることを意味します。実際、この例の０次コホモロジー群 $H^0$ は

$H^0=\{$ 左の島上の定数関数 $\} \times \{$ 右の島上の定数関数 $\} \cong \Bbb{R}^2$

となります。

あとがき

ここからが面白いところではあるのですが、ひとまずここで一区切りしたいと思います^ ^

今日の記事を通して、コホモロジーの

ホモロジーよりも壮大なスケール観を持っている
ホモロジーを介さなくても、幾何的な意味を持って構成できる

という側面を垣間見ていただけたなら嬉しいです♪

今回の話は、この後も

３つめの観測方法と１次コホモロジーの意味
ド・ラームコホモロジーとの関係性

という風に展開したいので、あと２回は続けるつもりです。よかったらお付き合いください^ ^♪

*1:一般には、「０次チェイン複体（＝頂点全体が生成するベクトル空間）から $\Bbb{R}$ への線形写像」を(実数係数の)０次コチェインと呼びます。

*2:今日は $H^0$ に代数構造を入れていませんが、‘‘ $\cong$ ”はベクトル空間の間の線形同型として正当化できます。

新米数学博士の数学談話室

数学基礎論からじっくり議論するブログです。