小話Vol.1:ベクトル場とトポロジー①
こんにちは!ルシアンです。
今回は、前回予告した数学の小話をしてみたいと思います。
基礎論から地道に紡いでいくのも数学の楽しみの一つですが、先回りして面白い話だけ「つまみ食い」するのもいいものですよね^ ^
今回は、曲面上のベクトル場と曲面のオイラー数の関係について紹介したいと思います。
曲面上のベクトル場
先日、佐野 岳人さん (id:taketo1024)が「トポロジーへの招待」という素晴らしい記事を書かれていました。
そのシリーズの中では、曲面が切り貼りで作られていて、まるで工作をしているような気分になります。
これは、トポロジー的観点の大きな魅力の一つですね!
でも今回はちょっと視点を変えて、曲面を「世界の舞台」のような大きな視点で捉えてみましょう。
具体的には、閉曲面の上で「ベクトル場」を考えてみます。*1
「ベクトル場」は物理を学んだ方なら馴染みがあるかもしれませんが、一言でいうと「各点の上にベクトルが乗っかっている」というものです。


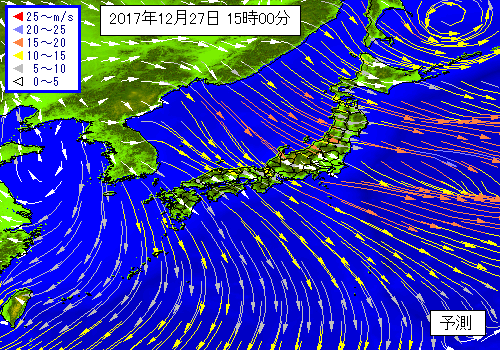
もしくは、曲面上の「気流」を考えていると思っていただいても構いません。下のような風予測図はベクトル場の一種です。
この曲面上の「気流」について、今日は次の問題を考えてみたいと思います。
問題:与えられた閉曲面上で、「風速0の地点」が一つもないような気流は存在するか?
これをもう少し数学的に述べると、
問題:与えられた閉曲面上で「零ベクトルが現れないベクトル場」は存在するか?
という問題になります。
具体例として、図1の2つのベクトル場について、風速0地点(零ベクトルが乗っている点)を観察してみましょう。


まず、トーラスの例ですが、それぞれのベクトルはメリディアンと呼ばれる円周に沿っていて、どれも大きさは0ではありません。
したがって、トーラス上には「零ベクトルが表れないベクトル場」が存在するとわかります。
では、球面の例の方を見てみましょう。
この球面を地球に見立てると、それぞれのベクトルは緯線の方向を向いており、赤道から離れるほどベクトルの大きさは小さくなっています。
すると、北極と南極ではベクトルの大きさが0になることが想像できるでしょう。実際、このベクトル場を正確に記述すると、2つの極では零ベクトルになります。
したがって、このベクトル場は「零ベクトルが表れるベクトル場」ということになります。
しかし、この観察だけでは「球面上で『零ベクトルが現れないベクトル場』は存在しない」とは言い切れません。
何故なら、今観察したのは、無数にある球面上のベクトル場のうちのたった一つしか考えていないからです。
「球面上で『零ベクトルが現れないベクトル場』が存在しない」ということを証明するには、無数にある全てのベクトル場を調べなければなりません。
ベクトル場とオイラー数
「曲面上の無数のベクトル場を調べる」というのは非常に骨が折れる問題に思えますよね。
しかし、オイラー数はこの問題に非常に美しい答えを与えてくれるのです。
定理:任意の閉曲面について、次のことが成り立つ。
上で「零ベクトルが現れないベクトル場」が存在する
のオイラー数は0
オイラー数が0の閉曲面はトーラスとクラインの壺しかありません。したがって、この定理から「零ベクトルが現れないベクトル場」がとれる閉曲面はこの二つしかないことが分かります。
特に、球面上では「風速0地点が一つもない気流」は存在しないと分かるのです。
例えば、あなたの見渡せる範囲が強風に見舞われているとします。このとき、「地球が丸い」という事実から「見えてないところに必ず無風地帯がある」という結論が出せるのです!
このように、
「世界の舞台」の大域的な形状が、ある地点の様子を決めてしまう
という現象も、トポロジーを通して知ることができます。
あとがき
今回は証明無しで定理を一つ紹介しただけだったので、少し内容が薄かったかもしれません^^;
近いうちに、「ベクトル場とトポロジー②」と題して、上の定理の証明に少し迫ってみたいと思います。
今回の記事は
を参考に書いています。
ブログの更新頻度、分量、前提知識など、いろいろ模索中です(>_<)ご要望がありましたらブログ・ツイッターでコメントください^ ^♪
この後は、少し詳しい方向けの付録です。
付録:一般の閉多様体について
今日紹介した定理は、一般の閉多様体についても成り立ちます。
すなわち、
定理:任意の閉多様体について、次のことが成り立つ。
上で「零ベクトルが現れないベクトル場」が存在する
のオイラー数は0
特に、向き付け可能な奇数次元閉多様体のオイラー数はつねに0になるので(ポアンカレ双対定理から従います)、次の系が得られます。
系:向き付け可能な奇数次元閉多様体上には、必ず「零ベクトルが現れないベクトル場」が存在する。
一方、次元球面
のオイラー数は2なので、
系:上では「零ベクトルが現れないベクトル場」は存在しない。
という系も成り立ちます。
*1:正確には、本記事では「滑らかな接ベクトル場」を考えています。