2017-12-28

小話Vol.1:ベクトル場とトポロジー①

小話トポロジー

こんにちは！ルシアンです。

今回は、前回予告した数学の小話をしてみたいと思います。

基礎論から地道に紡いでいくのも数学の楽しみの一つですが、先回りして面白い話だけ「つまみ食い」するのもいいものですよね^ ^

今回は、曲面上のベクトル場と曲面のオイラー数の関係について紹介したいと思います。

曲面上のベクトル場

先日、佐野岳人さん (id:taketo1024)が「トポロジーへの招待」という素晴らしい記事を書かれていました。

そのシリーズの中では、曲面が切り貼りで作られていて、まるで工作をしているような気分になります。

これは、トポロジー的観点の大きな魅力の一つですね！

でも今回はちょっと視点を変えて、曲面を「世界の舞台」のような大きな視点で捉えてみましょう。

具体的には、閉曲面の上で「ベクトル場」を考えてみます。*1

「ベクトル場」は物理を学んだ方なら馴染みがあるかもしれませんが、一言でいうと「各点の上にベクトルが乗っかっている」というものです。

f:id:Lucien0308:20171228051926g:plain — 図1：トーラス上のベクトル場（左）と球面のベクトル場（右）

f:id:Lucien0308:20171228010338g:plain — 図1：トーラス上のベクトル場（左）と球面のベクトル場（右）

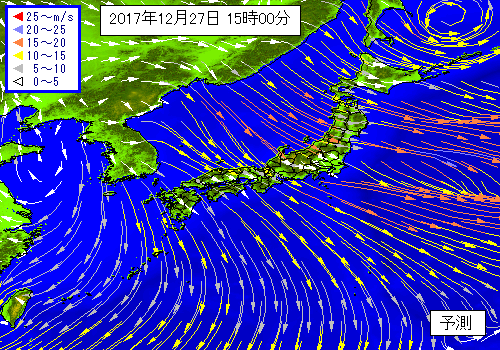
もしくは、曲面上の「気流」を考えていると思っていただいても構いません。下のような風予測図はベクトル場の一種です。

Sunny Spot 天気・気象情報サイト!より引用

この曲面上の「気流」について、今日は次の問題を考えてみたいと思います。

問題：与えられた閉曲面上で、「風速０の地点」が一つもないような気流は存在するか？

これをもう少し数学的に述べると、

問題：与えられた閉曲面上で「零ベクトルが現れないベクトル場」は存在するか？

という問題になります。

具体例として、図１の２つのベクトル場について、風速0地点(零ベクトルが乗っている点)を観察してみましょう。

まず、トーラスの例ですが、それぞれのベクトルはメリディアンと呼ばれる円周に沿っていて、どれも大きさは０ではありません。

したがって、トーラス上には「零ベクトルが表れないベクトル場」が存在するとわかります。

では、球面の例の方を見てみましょう。

この球面を地球に見立てると、それぞれのベクトルは緯線の方向を向いており、赤道から離れるほどベクトルの大きさは小さくなっています。

すると、北極と南極ではベクトルの大きさが０になることが想像できるでしょう。実際、このベクトル場を正確に記述すると、２つの極では零ベクトルになります。

したがって、このベクトル場は「零ベクトルが表れるベクトル場」ということになります。

しかし、この観察だけでは「球面上で『零ベクトルが現れないベクトル場』は存在しない」とは言い切れません。

何故なら、今観察したのは、無数にある球面上のベクトル場のうちのたった一つしか考えていないからです。

「球面上で『零ベクトルが現れないベクトル場』が存在しない」ということを証明するには、無数にある全てのベクトル場を調べなければなりません。

ベクトル場とオイラー数

「曲面上の無数のベクトル場を調べる」というのは非常に骨が折れる問題に思えますよね。

しかし、オイラー数はこの問題に非常に美しい答えを与えてくれるのです。

定理：任意の閉曲面 $S$ について、次のことが成り立つ。

$S$ 上で「零ベクトルが現れないベクトル場」が存在する $\Leftrightarrow$ $S$ のオイラー数は0

オイラー数が０の閉曲面はトーラスとクラインの壺しかありません。したがって、この定理から「零ベクトルが現れないベクトル場」がとれる閉曲面はこの二つしかないことが分かります。

特に、球面上では「風速０地点が一つもない気流」は存在しないと分かるのです。

例えば、あなたの見渡せる範囲が強風に見舞われているとします。このとき、「地球が丸い」という事実から「見えてないところに必ず無風地帯がある」という結論が出せるのです！

このように、

「世界の舞台」の大域的な形状が、ある地点の様子を決めてしまう

という現象も、トポロジーを通して知ることができます。

あとがき

今回は証明無しで定理を一つ紹介しただけだったので、少し内容が薄かったかもしれません^^;

近いうちに、「ベクトル場とトポロジー②」と題して、上の定理の証明に少し迫ってみたいと思います。

今回の記事は

田村一郎「岩波講座　基礎数学　微分位相幾何学II」、岩波書店

を参考に書いています。

ブログの更新頻度、分量、前提知識など、いろいろ模索中です(>_<)ご要望がありましたらブログ・ツイッターでコメントください^ ^♪

この後は、少し詳しい方向けの付録です。

付録：一般の閉多様体について

今日紹介した定理は、一般の閉多様体についても成り立ちます。

すなわち、

定理：任意の閉多様体 $M$ について、次のことが成り立つ。

$M$ 上で「零ベクトルが現れないベクトル場」が存在する $\Leftrightarrow$ $M$ のオイラー数は0

特に、向き付け可能な奇数次元閉多様体のオイラー数はつねに0になるので（ポアンカレ双対定理から従います）、次の系が得られます。

系：向き付け可能な奇数次元閉多様体上には、必ず「零ベクトルが現れないベクトル場」が存在する。

一方、 $2n$ 次元球面 $S^{2n}$ のオイラー数は2なので、

系： $S^{2n}$ 上では「零ベクトルが現れないベクトル場」は存在しない。

という系も成り立ちます。

*1:正確には、本記事では「滑らかな接ベクトル場」を考えています。

2017-12-24

基礎論Vol.3:なぜ「公理的集合論」は必要なのか？

公理的集合論数学基礎論

メリークリスマス！

こんにちは、ルシアンです。

前回は予定を変更して、記号論理学の解説を少し掘り下げてみました。

(前回→基礎論Vol.2:もう少しだけ記号論理学 - 新米数学博士の数学談話室)

その内容をまとめると、次のようになります。

記号の種類は３種類。論理記号は全ての理論で、特殊記号はそれぞれの理論で最初に定められる。文字は自由に設定できる。
数学で用いることが出来る「名詞」と「命題」は、記号列でなければならない。
記号列は、５つのルールにしたがって、順次構成することしかできない。
「証明」は、公理から順番に「真」の命題を増やしていく事で与えられる。
全ての数学で、５つの論理学の公理があらかじめ設定されている。

今回からはいよいよ、「公理的集合論」について議論していきたいと思います。

記号論理学で、素朴に集合の定義を考えると…？

まず、高校での集合の定義をもう一度思い出してみると、

「定義が具体的に示されているモノの集まり」

というものでした。

この定義を見ると、次の概念を記号化する必要がありそうです。

「モノ」
「具体的な定義」
「モノの集まり」

これらに対して、私たちは相応しいであろう答えを、すでにもっています。つまり、

「モノ」

→全ての名詞 $T$ を「モノ」とみなす。

「具体的な定義」

→命題 $P$ について、「 $P|_{x=T}$ が真となる名詞 $T$ 全体」を集合の定義にする。*1

「モノの集まり」

→重み２の特殊記号 $\in$ を導入して、「 $T$ が $S$ の元」であることと「 $T \in S$ が真」であることが同値になるようにする。*2

としてみれば、とても素朴に集合が定義できそうです。

実は、この考えはあながち間違っていません。実際、

‘‘公理”：任意の命題 $P$ について、「 $^{\exists}S, ^{\forall} x, (\ x \in S \Leftrightarrow P)$ 」を真とする。

（すなわち、 $P|_{x=T}$ をみたす名詞 $T$ 全体の集合 $S$ が存在する）

を導入すれば、いわゆる「ZFC公理系」はすべて、ごく自然に満たされるのです！

しかし、この‘‘公理”にはとんでもない落とし穴が潜んでいます。というのも、この公理による集合論は矛盾した理論になってしまうのです。

集合論の落とし穴：ラッセルのパラドックス

記号論理学における「矛盾」とは？

「落とし穴」について解説する前に、まずは「矛盾した理論とはなにか？」についてお話したいと思います。

記号論理学では、公理系を一つ選ぶごとに、どの命題が真になるかが確定します。

では、真でない命題は「偽」となるんでしょうか？

実は、そうとも言い切れないのです。どういうことか見ていきましょう。

記号論理学の初めに、論理記号 $\lnot$ を導入しました。これを用いることで、

「命題 $P$ が偽」

であることは

「命題 $\lnot P$ が真」

であることとして定義されます。

一方で、ある公理系の命題が真かどうかは、公理から「証明プロセス」によってその命題にたどり着けるかどうかで決まっていました。

これは、

$P$ と $\lnot P$ が真かどうかは独立である

つまり

$P$ と $\lnot P$ はともに真になり得る

ということを意味しています。

一般に「 $P$ と $\lnot P$ の一方は真で、もう一方は真ではない」という規則を無矛盾律といいます。

記号論理学では、 $P$ と $\lnot P$ が真であることの定義が独立しているため、一般に無矛盾律が成り立つことは保証できないのです。

そこで、矛盾した理論を次のように定めます。

定義：与えられた公理系において、ある命題 $P$ とその否定 $\lnot P$ の両方が真であると証明できるとき、その公理系を矛盾した理論とよぶ。

この矛盾した理論というのがどれくらいまずいかというと、「全く使い物にならない」ということが分かります。実際、次のことが確かめられます。

事実：矛盾した理論においては、全ての命題が真となる。

（この事実の証明は、本記事の付録にしたいと思います。）

これは、「全ての命題とその否定の両方が証明できる」ことを意味しているため、結局ひとつも真偽の結論を下せない理論という事になってしまいます。

よって、今考えている集合論も、「ZFC公理系」を満たすどころか、ZFC公理系の否定も含めてすべての命題とその否定が証明されてしまう「結論のない理論」ということになってしまいます。

ラッセルのパラドックス

それでは、今考えている集合論が「矛盾した理論」であることを、実際に証明してみましょう。

１．まず、文字 $x$ に対して命題「 $x \notin x$ 」を考えます。

（正確には「 $\lnot (x \in x)$ 」という命題です。）

２．次に、上述の‘‘公理”を使って、命題 $x \notin x$ に対応する集合 $S$ を得ます。普段の表記だと、 $S$ は

$S=\{x \mid x \notin x \}$

という集合です。

３．一方、 $S$ 自身も名詞ですから、「 $S \in S$ 」は命題です。ここで、次の事実を証明しましょう。

事実： $S \in S$ と $S \notin S$ はともに真。

[証明]　まず、論理学の公理系から、

全ての命題 $P$ について、 $P\lor \lnot P$ と $\lnot P\lor P$ は真である。
全ての命題 $P$ について、 $P \Rightarrow P$ は真である。

場合分けの証明法：命題 $A\lor B$ , $A \Rightarrow C$ , $B \Rightarrow C$ が全て真ならば、命題 $C$ も真である。

の三つの事実が確かめられます。（普段ならどれも当たり前に思える推論ですね。）

これらを組み合わせると、次の事実が分かります：

$P \Rightarrow \lnot P$ かつ $\lnot P \Rightarrow P$ が真ならば、 $P$ と $\lnot P$ はともに真である。

（例えば、 $P$ が真であることを示したければ、 $A= \lnot P, B = C=P$ を代入してみてください。）

したがって、ここでは「 $S \in S \Rightarrow S \notin S$ かつ $S \notin S \Rightarrow S \in S$ 」が真であることを証明できればよいという事になります。

しかし、これも簡単に証明できてしまうのです。なぜなら、 $S$ の定義から全ての名詞 $T$ について

$T \in S \Leftrightarrow T \notin T$

が真となり、この $T$ に $S$ を代入すれば

$S \in S \Leftrightarrow S \notin S$

が真となるからです。命題「 $P \Leftrightarrow Q$ 」はそもそも「 $P \Rightarrow Q$ かつ $Q \Rightarrow P$ 」

という命題の略記であるため、上の考察から題意は示されました。

（証明終了）

これで、今考えている集合論が「矛盾した理論」であることが証明できてしまいました。

この議論を一般化すると、次のラッセルのパラドックスが得られます。

ラッセルのパラドックス： $\{x \mid x \notin x \}$ が集合として扱われる「集合論」は、すべて矛盾した理論となる。

ラッセルのパラドックスを回避するには？

今回考えた集合論が矛盾してしまった原因はどこにあったのか、振り返ってみましょう。

それは、 $\{x \mid x \notin x \}$ を集合として扱ってしまった、つまり集合の定義が広すぎたということが問題だったと言えます。

なので、この問題を回避するためには集合の定義を狭める必要があるということになります。

しかし一方で、集合の定義を狭めすぎてしまうと、実数全体の集合 $\Bbb{R}$ など、集合として扱いたいモノが定義からはみ出てしまうという別の問題が発生してしまいます。

したがって、この挟み撃ちをクリアできる集合論を考えなければならず、それに成功したのが「ZFC公理系」によって定められる公理的集合論なのです！

f:id:Lucien0308:20171224023255g:plain

おわりに

今回はラッセルのパラドックスを通して、「公理的集合論の必要性」を解説してみましたが、いかがだったでしょうか？

問題に板挟みにされ、その解決に苦心した数学者たちの姿が垣間見えたなら本望です。

次回からは、ZFC公理系の各公理について、順番に紹介していきます。

また、記事を準備しながら思ったことについての雑記や、自分の得意な位相幾何学に関する小話なども、今後は混ぜていく予定です。

意見、感想、リクエストなどは本記事やツイッターでコメントください^^♪

このあとは付録です。

付録：「矛盾した理論においては、全ての命題が真となる。」の証明

[証明]まず、矛盾した理論であることから、「 $A$ と $\lnot A$ がともに真」となる命題 $A$ が存在します。この $A$ を用いて、任意の命題が真であることを証明しましょう。

（論理学の公理や「証明」のルールについては、前回の記事をご覧ください。）

$B$ を任意の命題とします。このとき、論理学の公理２により

$\lnot A \Rightarrow \lnot A \lor B$

は真となります。また、 $\lnot A$ も真であることから、「証明」のルール２により $\lnot A \lor B$ も真であることが分かります。

ところで、 $\lnot A \lor B$ は「 $A \Rightarrow B$ 」の定義だったわけですから、命題 $A \Rightarrow B$ が真だということになります。

ここで、 $A$ も真であることから、再び「証明」のルール２によって $B$ が真であるとわかります。　（証明終了）

*1: $P$ が文字 $x$ を含まないときは、 $P|_{x=T}$ は $P$ と同じ命題になります。

*2: $T \in S$ は、記号論理学的には $\in T S$ と書くのが正しい表記ですが、必要な時に置き換えることにしておけば問題はありません。

2017-12-21

基礎論Vol.2:もう少しだけ記号論理学

数学基礎論記号論理学

こんにちは！ルシアンです。

前回は

数学基礎論とは「違う言葉で書かれた数学を『翻訳する』ための方法論」である。
具体的には、数学で扱う全てのモノ・命題・推論などを「記号の列」に置き換える。
この置き換えのルールは「記号論理学」によって定められている。

ということについてお話ししました。

(前回→基礎論Vol.1:そもそも「数学基礎論」とはなにか？ - 新米数学博士の数学談話室)

前回の最後に、次回は「なぜ『公理的集合論』は必要か？」というテーマで書くと言いましたが、あまりに記号論理学がブラックボックス過ぎるのも分かりづらいなと思い直しました。

ということで、今日は記号論理学についてもう少しだけ掘り下げたいと思います。

※内容が少しマニアックかもしれません。最後に「まとめ」を設けるので、面倒な方はそれだけ見て下さい(^^)

記号の種類

まずは、前回全く述べなかった、記号列を成す記号たちについて紹介します。

実のところ、記号は次の3種類しかありません。

１．論理記号： $\tau,\lor,\lnot$

全ての理論で導入される、もっとも基本的な記号です。意味は後述します。

２．文字： $x,y,z,\ldots$

意味を持たない「名詞」です。例えば、１つの命題の中でxを一斉に「Aくん」に取り換えても命題の真偽は変わりません。

３．特殊記号： $=,\in, \subset, \ldots$

各理論ごとに導入される記号です。それぞれに重みという自然数 *1が設定されています。重みの意味は後述します。

記号列の構成ルール

上の3種類の記号を並べて「記号列」を作るわけですが、デタラメに並べたものは「記号列」とは認めません。

記号列の作り方は非常に制限されていて、たった5種類しかありません。このルールを有限回適用して得られる列のみが「記号列」と認められます。

また、記号列には

「名詞」に当たるもの
「命題」に当たるもの

の2種類があり、以下のどのルールを使うかで、得られた記号列が「名詞」か「命題」かが決まります。

１．一つの文字を「名詞」の記号列とみなす。

ただし、ここでいう「文字」は記号の種類を指しています。

２． $A$ という命題があったら、列 $\lnot A$ も「命題」の記号列とみなす。

$\lnot A$ は「 $A$ の否定」にあたる命題です。

３． $A,B$ という二つの命題があったら、列 $A \lor B$ も「命題」の記号列とみなす。

$A \lor B$ は「 $A$ または $B$ 」にあたる命題です。

４．文字 $x$ を含む命題 $A$ があったら、列 $\tau x A$ を「名詞」の記号列とみなす。

$\tau x A$ は「命題 $A$ における $x$ の役割を果たすもの」という名詞です。見慣れないかもしれませんが、この名詞から存在記号 $\exists$ と任意記号 $\forall$ の両方を作り出すことができます。

５． $n$ 個の名詞 $A_1, A_2,\ldots, A_n$ と重み $n$ の特殊記号 $s$ があったら、列 $sA_1A_2\cdots A_n$ を「命題」の記号列とみなす。

例えば、 $=,\in, \subset$ は全て重み２の特殊記号で、命題「 $=A_1A_2$ 」は普段の記法だと「 $A_1=A_2$ 」を意味します。

「本当にこの５つのルールだけで、全ての数学に必要な『名詞』と『命題』が作れるの？」

と思うかもしれませんが、それができてしまうのです。（作った人達天才すぎる…）

たとえば、

「 $A$ かつ $B$ 」 $:=$ $\lnot\left( (\lnot A) \lor (\lnot B)\right)$
「 $A \Rightarrow B$ 」 $:=$ $(\lnot A) \lor B$
「 $^{\exists}x, A$ （命題 $A$ を満たす $x$ が存在する）」 $:=$ $A|_{x=\tau x A}$
「 $^{\forall}x,A$ （任意の $x$ について $A$ が成り立つ）」 $:=$ $\lnot (\lnot A|_{x=\tau x\lnot A})$

などと表すことが出来ます。*2

ただし、 $A|_{x=\tau x A}$ は命題 $A$ の中の $x$ を全て $\tau x A$ で置き換えて得られる列です。*3

記号列の運用法：記号論理学における「証明」とは何か？

これで、現代数学において扱うことのできる「名詞」と「命題」の限界を定めることが出来ました。

しかし、今のままでは使用可能な‘‘言葉”が定まっただけであって、

「与えられた仮定から推論を繰り返し、結論を導く」

という証明のプロセスがはっきりしていません。

そこで、記号論理学における「証明」を次のように定めます。

１．いくつかの命題*4を公理に設定する。

２．公理に設定された命題は「真」と考える。

３．命題 $A$ と「 $A \Rightarrow B$ 」が「真」であるとき、命題 $B$ も「真」とする。

４．２と３を有限回適用して命題 $P$ が「真」とされたとき、真と認められた命題を順に並べたものを「 $P$ の証明」とよぶ。

これで、「名詞」や「命題」のみならず「証明」さえも記号の列にすることができました…！

今後、数学の定義・主張・証明などに曖昧さを感じたときは、上述の記号列の意味で正しいかどうかをチェックすればよいことになります。

論理学の公理系

最後に、論理和 $\lor$ ，否定 $\lnot$ ，存在記号 $\exists$ が本来の意味を持つように、「論理学の公理系」を定めれば完成です。

この「論理学の公理系」は今後全ての数学で仮定されているものとなります。

（この先深く踏み入らないので読み流してOKです。）

１．命題 $A$ について、「 $A \lor A \Rightarrow A$ 」を公理とする。

２．命題 $A,B$ について、「 $A \Rightarrow (A \lor B)$ 」を公理とする。

３．命題 $A,B$ について、「 $(A \lor B) \Rightarrow (B \lor A)$ 」を公理とする。

４．命題 $A,B,C$ について、「 $(A \Rightarrow B) \Rightarrow \left( (C \lor A) \Rightarrow (C \lor B)\right)$ 」を公理とする。

５．命題 $A$ 、名詞 $T$ 、文字 $x$ について、「 $A_{x=T} \Rightarrow ( ^{\exists}x, A)$ 」を公理とする。

これらの公理に上述の「証明」のプロセスを適用して得られる「真」の命題が、今後証明の中で用いることができる「推論」ということになります。

まとめ

今回は様々なルールを具体的に書き下したため、追うのがやや面倒な内容になってしまったかもしれません。

しかし、このプロセスを知るだけでも現代数学の価値観が垣間見えると思うので、見出しだけでも追ってもらえれば嬉しいです＾＾

今日の議論をまとめると、以下のようになります。

記号の種類は３種類。論理記号は全ての理論で、特殊記号はそれぞれの理論で最初に定められる。文字は自由に設定できる。
数学で用いることが出来る「名詞」と「命題」は、記号列でなければならない。
記号列は、５つのルールにしたがって、順次構成することしかできない。
「証明」は、公理から順番に「真」の命題を増やしていく事で与えられる。
全ての数学で、５つの論理学の公理があらかじめ設定されている。

次回からはいよいよ、準備した記号論理学の上で「集合論」を展開していきたいと思います。そのプロセスには様々な困難やドラマがあるので、それらを一緒に体験できればうれしいです！

※今回の話は全て

ブルバキ「数学原論　集合論I」、東京図書

をもとに書いていますが、より直観的に理解できるようにするため、言葉遣いや記法には手を加えています。ご自分で読まれる際はご注意ください。

*1:ここでいう自然数は数学的対象ではなく、単なる個数です。

*2:記号列内の括弧は見やすさのために入れているもので、本来はありません。

*3:一般に、命題内の文字に他の名詞を‘‘代入”した列はつねに「命題」の記号列になります。

*4:シェーマという概念を用いることで、有限個のルールから無限個の命題を公理に設定することができます。

2017-12-18

基礎論Vol.1:そもそも「数学基礎論」とはなにか？

数学基礎論記号論理学

こんにちは、ルシアンと申します。唐突に始めたブログですが、まず１つ記事を書いてみたいと思います。

テーマは、「そもそも『数学基礎論』とはなにか？」です。

※以下の内容は、「そう考えると数学基礎論って必要だね」と思える一つの見方を書いたものです。個人の一意見として捉えてください。

数学における「文化」や「言語」の問題

中高の数学を勉強していて、「単元ごとに基礎になっている価値観がちがう？」みたいに思ったことはないでしょうか？

たとえば、「三平方の定理」とか「円や特別な三角形の性質」を勉強する時は、点と円と直線くらいしかでてきませんが、「円や直線の方程式」の時にはつねにxy座標が指定されていたりします。

かと思えば、違う章では「直線の方程式」は1次関数とよばれたりしているわけです。

このように価値観や呼び方が入り混じっているのは、違う時代・背景のもとで生まれた数学が入り混じっているからです。

なので、自分は高校の教科書を見ると「色々な民族が同じ敷地に閉じ込められている」というような印象を持ちます。

そして、発展問題などで、関数の問題の解法で突然図形の性質が出てきたりすると「そんなのありなの？」という気分になります。

この現象をまとめると次のようになります。

一言で数学と言っても、時代・背景によって様々な価値観・文化がある
しかし「問題を解く」という価値観は共通しており、その解法が突然他の文化圏から飛んできたりする

ある文化圏の人々が頭を抱えていた問題を、別の文化圏の人々が異文化のルールで解けたと言っていても、素直に認めたくないですよね。

なので、「異文化間の言葉やルールを『翻訳する』確かな方法」が必要になります。

それを与えているのが「数学基礎論」なのです。

記号論理学：すべての数学に共通する基礎づけを！

では、どのような方法で『翻訳』するのが適当でしょうか？

これに対して数学者たちが出した答えが

「『言葉』と『ルール』をつかさどる、最も抽象的な数学*1をつくる」

ということでした。これを「記号論理学」といいます。

この記号論理学というのは本当にすごくて、数学で取り扱うモノ・概念・推論などをすべて「記号の列」に翻訳することができます。

例えば「AかつB」とか「AならばB」などの推論も、全て記号の列になってしまいます。

基本的な概念を記号列に翻訳したら、今度は「記号列の基本ルール」を定めます。そして、証明の正しさというのは全て「記号の並びがルールから外れていないか」の確認に帰着されるのです。

（この「記号列の基本ルール」というのもかなり単純で、記号列の長さを度外視すれば、証明の正しさをコンピュータに確かめさせることも容易だと思います。）

これによって、記号論理学は数学の「標準語」の役割を担うことになります。

実際、ある文化の問題や証明を翻訳する時は、

ある数学文化での言葉遣い→[記号論理学]→記号列→[記号論理学]→別の数学文化での言葉遣い

という風に翻訳できるわけです。

そして、例えばまっさらな平面上の図形の問題を、座標を導入して解いたとしても、記号論理学的に正しければOKということになります。

記号論理学とどう向き合うべきか？

記号論理学のおかげで、数学には「標準語」というべきものが与えられました。

そうすると、「普段から標準語で話せば便利じゃない？」と思うかもしれません。しかし、普段扱う数学を記号列にすると恐ろしく長い上に、数学の背景や直観的見方が失われてしまいます。

なので、一つ一つの概念をいちいち翻訳することはあまり有益でないと思われます。

では、記号論理学とどのように向き合えばよいでしょうか？ここではその一例を挙げます。

１．数学の限界を知る

例えば、高校では集合を「定義が具体的に示されているモノの集まり」などと定めますが、「モノって、本当になんでもいいの？」となりますよね。

記号論理学をかじれば、こういう疑問にも答えが出せます。

たとえば、「Aくん」を集合の元として扱うとき、「『Aくん』とよばれるただの文字」として扱うのは記号論理学では非常に容易です。

ただし、この場合は「Aくん」自身の性質は全く反映されず、「Aくん」と呼ぶことと「x」と呼ぶことには何の差も生まれません。

一方、例えば「人間としての『Aくん』」を数学で扱うためには、まず「人間」を記号列にしなければなりません。

この様にして考えると、何が数学的な「モノ」として扱えるかが鮮明に見えてくるのではないでしょうか？

２．問題を翻訳する

例えば、

「『まっさらな平面上の図形の問題*2』を『座標を導入』して解く」

ということをしたいとき、厳密には

「座標を導入するかしないかで結論は変わらない」

ということを保証しなければなりません。

これはどのようにすれば解決できるか？というのは、今後の具体的な議題にしてもよいですね。

おわりに

今回は「記号論理学」の話が中心的なテーマとなりましたが、次回以降は議論の根拠として引用するのみになると思います。

自分で詳しく学びたいという方は、以下の文献を開いてみて下さい。

ブルバキ「数学原論　集合論I」、東京図書
上野健爾，砂田利一，深谷賢治，神保道夫「岩波講座　現代数学への入門　現代数学の流れ１」、岩波書店

次回は、「なぜ『公理的集合論』は必要か？」というテーマで書くつもりです。

今回の感想や意見、今後の記事の要望などがあれば、こちらの記事にコメントか、質問箱（https://peing.net/lucien0308）にてお知らせください♪

次→もう少しだけ記号論理学 - 新米数学博士の数学談話室

*1:正しくは論理学というべきかもしれません。

*2:すなわち、ユークリッド幾何の問題です。

曲面上のベクトル場

ベクトル場とオイラー数

あとがき

付録：一般の閉多様体について

記号論理学で、 素朴に集合の定義を考えると…？

集合論の落とし穴：ラッセルのパラドックス

記号論理学における「矛盾」とは？

ラッセルのパラドックス

ラッセルのパラドックスを回避するには？

おわりに

付録：「矛盾した理論においては、全ての命題が真となる。」の証明

記号の種類

記号列の構成ルール

記号列の運用法：記号論理学における「証明」とは何か？

論理学の公理系

まとめ

数学における「文化」や「言語」の問題

記号論理学：すべての数学に共通する基礎づけを！

記号論理学とどう向き合うべきか？

１．数学の限界を知る

２．問題を翻訳する

おわりに

記号論理学で、素朴に集合の定義を考えると…？